티스토리 뷰
분류(Classification)란?

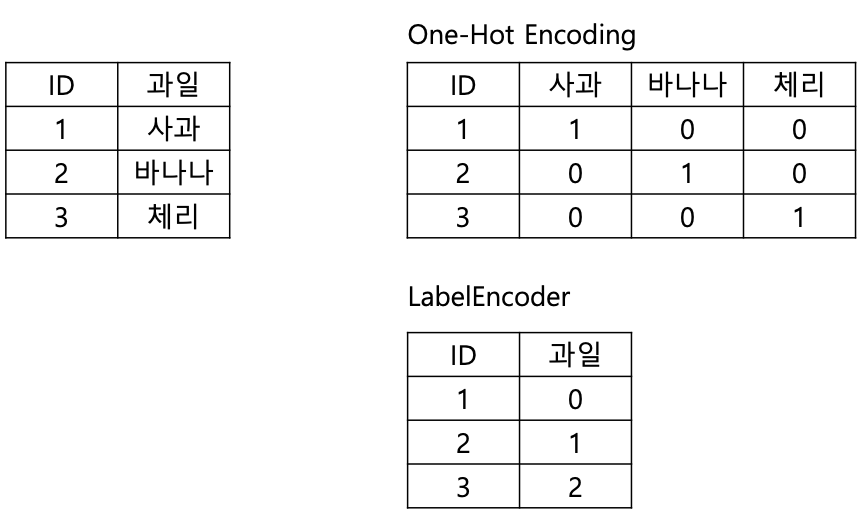
입력 벡터 $\textbf{x}$가 주어졌을 때 이를 $K$개의 이산 클래스 $C_{k}$들 중 하나에 할당하는 것이다. Regression은 타깃 변수(target variable)이 예측하고자 하는 실수였지만, classification은 명확한 class를 표현해야 하므로 다양한 방식으로 타깃 변수를 사용한다. 표현 방법 중 한가지가 원 핫 인코딩(one hot encoding)이다.
input space는 결정 경계(decision boundary) 혹은 결정 표면(decision surface)이라고 불리우는 경계를 바탕으로 여러개의 결정 구역으로 나눠지게 된다.
선형 모델로 해결하는 방법
분류문제는 두 개의 단계로 나눌 수 있다(1.5.4 참고). 추론 단계(inference stage)는 training set을 이용하여 $p(C_{k}|\textbf{x})$에 대한 모델을 학습시키는 단계이고, 결정 단계(decision stage)는 앞에서 학습된 사후 확률을 이용해 최적의 클래스 할당을 시행하는 것이다. 이 단원에서 아래와 같은 방법에 대해 설명한다.
- 각각의 벡터 x를 특정 클래스에 바로 배정하는 방법. 추론과 결정 단계를 한번에 풀어내는 방식이다.
- 판별함수(Discriminant Function)
- 추론 단계에서 조건부 확률분포를 모델링하는 방법.
- 확률적 판별 모델(Probabilistic Discriminative Models): 사후 확률 $p(C_{k}|\textbf{x})$을 직접 모델
- 확률적 생성 모델(Probabilistic Generative Models): 클래스에 대한 조건부 확률밀도$p(\textbf{x}|C_{k})$를 알아내는 추론 문제를 풀고, 클래스별 사전 확률을 따로 구해서 베이지안 정리로 클래스별 사후확률 $p(C_{k}|\textbf{x})$을 구하는 방법
4.1 판별 함수(Discriminant Function)
판별 함수를 구할 수 있는 세 가지 방법을 설명한다.
- 최소 제곱법
- 피셔의 선형 판별
- 퍼셉트론 알고리즘
4.1.1 두 개의 클래스
가장 단순하게 표현한 선형 판별 함수는 아래와 같다.
$$y(\textbf{x})=\textbf{w}^{T} \textbf{x} + w_{0}$$
클래스가 두 개인 경우 $y(\textbf{x})$가 양수이면 클래스 $C_{1}$에 배정하고, 음수이면 $C_{2}$에 배정한다. 이 경우 결정 경계(결정 표면)는 $y(\textbf{x})=0$이 되며, 이는 $D$차원 입력 공간 상의 $(D-1)$차원의 초평면(hyperplane)에 해당한다. 이 초평면을 구하는 방법을 알아보자.
결정 표면상의 임의의 두 점 $x_{A}$와 $x_{B}$를 생각해보자(이미지에서 보라색 선). $y(x_{A})=y(x_{B})=0$이므로 $\textbf{w}^{T}(x_{A}-x_{B})=0$이다. 이로부터 $\textbf{w}$가 결정 표면상의 모든 벡터들과 직교하며, 결정 표면의 모양을 결정한다는 것을 알 수 있다.
결정 표면까지의 수직 최단거리는 $\frac{\textbf{w}^{T}\textbf{x}}{\left| \textbf{w} \right|}$ 이고, 이것은 $-\frac{w_{0}}{\left| \textbf{w} \right|}$과 같다. 따라서 편향 매개변수 $w_{0}$이 결정 표면의 위치를 정한다는 것을 알 수 있다(검정색 선).
$y(\textbf{x})$의 값(입력값이 결정 평면과 얼마나 떨어져 있는가)은 점 $\textbf{x}$와 수직 거리 $r$에 비례한다.

표기를 간단하게 하기 위해 가변수 $x_{0}=1$을 사용해 아래와 같이 나타낼 수 있다. $\tilde{\textbf{w}}=(w_{0}, \textbf{w})$이고, $\tilde{\textbf{x}}=(x_{0}, \textbf{x})$이다.
$$y(\textbf{x})=\tilde{\textbf{w}}^{T}\tilde{\textbf{x}}$$
4.1.2 다중 클래스
두 개의 클래스의 방식을 확장해서 $K$개의 클래스 각각에 대한 $K$개의 판별 함수를 구한다. 두 개의 클래스일 때와 다른 점은 이 판별 함수의 비교를 통해 클래스를 배정한다는 것이다. $j\neq k$인 모든 $j$에 대해 $y_{k}(\textbf{x}) > y_{j}(\textbf{x})$면 포인트 $\textbf{x}$를 클래스 $C_{k}$에 배정하는 것이다. 클래스 $C_{k}$와 클래스 $C_{j}$ 사이의 결정 경계는 $y_{k}(\textbf{x}) = y_{j}(\textbf{x})$로 주어지며 이에 따른 초평면의 아래와 같이 정의된다.
$$(\textbf{w}_{k}-\textbf{w}_{j}^{\text{T}})\textbf{x}+(w_{k0}-w_{j0})$$
최소 제곱법
4.1.3 분류를 위한 최소 제곱법
제곱합 오류 함수를 최소화 하는 문제를 푸는 방식을 적용해보자. 최소 제곱법을 사용하는 것이 타당한 이유는 $\mathbb{E}\left [ \textbf{t}| \textbf{x} \right ]$의 근삿값을 구하는 방법이기 때문이다.
각각의 클래스 $C_{k}$들을 각각 선형 모델로 표현할 수 있다.
$$y_{k}(\textbf{x})=w_{k}^{\text{T}}\textbf{x} + w_{k0}$$
이 식을 벡터 표기를 이용해서 하나로 묶어주면 아래와 같다.
$$\textbf{y}(\textbf{x})=\tilde{\textbf{W}}^{\text{T}}\tilde{\textbf{x}}$$
$$ \tilde{\textbf{W}} = \begin{bmatrix}
\tilde{w}_{1}& \tilde{w}_{2} & \cdots & \tilde{w}_{K} \
\end{bmatrix}$$
위의 표현을 기반으로 정리한 제곱합의 오류함수는 아래와 같다.
$$E_{D}(\tilde{\textbf{W}})=\frac{1}{2} \textbf{Tr} ( (\tilde{\textbf{X}}\tilde{\textbf{W}} -\tilde{\textbf{T}})^{\textbf{T}}(\tilde{\textbf{X}}\tilde{\textbf{W}} -\tilde{\textbf{T}}))$$
$\tilde{\textbf{W}}$에 대한 미분값을 0으로 놓고 정리하면(유도 정리?) 아래와 같은 해를 구할 수 있다.
$$\tilde{\textbf{W}} = (\tilde{\textbf{X}}^{\textbf{T}}\tilde{\textbf{X}})^{-1}\tilde{\textbf{X}}^{\textbf{T}}\textbf{T} = \tilde{\textbf{X}}^{\dagger}\textbf{T}$$
특징
- 이상값이 주어졌을 때 강건성이 부족하다.
- 각 클래스마다 비교한 결정 경계가 존재해서 아래 그림과 같은 경우는 분류가 잘 되지 않는다. 이 경우 로지스틱 회귀를 사용해 분류하면 올바르게 분류되는 것을 볼 수 있다(오른쪽 그림). 최소 제곱볍이 원래 가우시안 조건부 분포를 가정하고 있어서 발생하는 문제이다.


피셔의 선형 판별
4.1.4 피셔의 선형 판별(Fisher’s linear discriminant)
차원 감소의 관점으로 살펴보면 다중 클래스에서 판별 함수는 입력 벡터를 1차원에 투영한 것이라 생각할 수 있다. 이렇게 투영을 하게되면 상당한 양의 정보를 잃게 되고, 심하게 겹칠 수 있다. 하지만 가중 벡터 $\textbf{w}$의 성분들을 잘 조절하면 분리를 최대화하는 투영을 선택할 수 있다. 이것이 피셔의 선형 판별이다.

$\textbf{w}$에 투영되었을 때 클래스 간의 분리된 정도를 측정할 수 있는 가장 쉬운 방법은 평균의 분리 정도를 살펴보는 것이다.
$$\begin{gather} m_{2}-m_{1} = \textbf{w}^{\textbf{T}}(\textbf{m}_{2} - \textbf{m}_{1}) \newline
m_{k} = \textbf{w}^{\textbf{T}}\textbf{m}_{k} \end{gather}$$
하지만 이렇게 평균의 분리만 비교하게 되면 $\textbf{w}$를 통해서 임의로 식의 값을 키울 수 있다. 라그랑주 승수법을 이용해 $\sum_{i}w_{i}^{2}=1$이 되도록 제약 조건을 넣어 극대화를 하면 $\textbf{w}\propto (\textbf{m}_{2} - \textbf{m}_{1})$라는 것을 알 수 있다. 하지만 이 방식도 아래 이미지 왼쪽과 같이 상당한 중복이 생기는 문제가 있다. 따라서 오른쪽 방법과 같이 클래스 내의 분산을 작게 하는 함수를 최대화하는 방식을 사용한다.

이것을 식으로 나타내면 아래와 같다. 이것을 피셔의 선형 판별 이라고 한다.
$$\textbf{w} \propto S_{W}^{-1}(\textbf{m2} - \textbf{m1})$$
이 식을 유도하는 과정을 다음과 같다.
클래스 내 분산 $s_{k}^{2} = \sum_{n\in C_{k}}(y_{n}-m_{k})^{2}$
피셔 기준 $J(\textbf{w}) = \frac {(m_{2}-m_{1})^{2}}{s_{1}^{2}+s_{2}^{2}}$
피셔 기준을 $\textbf{w}$에 종속적인 형태로 나타내면 $J(\textbf{w}) = \frac {\textbf{w}^{\textbf{T}}S_{\textbf{B}}\textbf{w}}{\textbf{w}^{\textbf{T}}S_{\textbf{W}}\textbf{w}}$
이 식을 $\textbf{w}$에 대해 미분하면 $(\textbf{w}^{\textbf{T}}S_{\textbf{B}}\textbf{w})S_{\textbf{W}}\textbf{w} = (\textbf{w}^{\textbf{T}}S_{\textbf{W}}\textbf{w})S_{\textbf{B}}\textbf{w}$
양변에 $S_{\textbf{W}}^{-1}$을 곱하면 위의 식을 얻게 된다.
피셔의 선형 판별 자체는 엄밀히 말하면 판별 함수가 아니라 투영을 하기위한 방향을 정하는 것이지만, 임계값 $y_{0}$를 정해서 분류를 하는 식으로 판별 함수를 만들 수 있다. 투영된 클래스들의 가우시안 근사를 찾아낸 후 1.5.1절의 오분류의 비율을 최소화하는 방식을 적용하면 임계값을 찾을 수 있다.

4.1.5 최소 제곱법과의 관계
피셔 기준은 최소 제곱법의 특별 케이스로 볼 수 있다. 원 핫 인코딩 대신 다른 부호화를 적용하면 최소 제곱해가 피셔해와 동일해진다.
클래스 $C_{1}$의 표적값을 $N/N_{1}$, 클래스 $C_{2}$의 표적값을 $-N/N_{2}$라고 하자. $N_{i}$는 각 클래스에 있는 패턴들의 수이고, $N$은 전체 패턴의 수이다. 이렇게 부호화 하면 피셔 기준의 가중치 벡터와 일치하게 된다.
유도 정리......
4.1.6 다중 클래스에 대한 피셔 판별식
입력 공간 $D$는 클래스의 수 $K$보다 크다고 가정한다. 그리고 $D' >1$개의 선형 '특징' $y_{k}=w_{k}^{\textbf{T}}\textbf{x}$를 도입한다. 이 특징 값들을 묶어 벡터 $\textbf{y}$를 표현할 수 있다. 이와 비슷하게 가중치 벡터 $w_{k}$를 행렬 $\textbf{W}$로 표현할 수 있다.
$$\textbf{W} = \begin{bmatrix}
w_{1}& w_{2} & \cdots & w_{D'} \
\end{bmatrix}$$
$$\textbf{y} = \textbf{W}^{\textbf{T}}\textbf{x}$$
두 개의 클래스가 존재했을 때와 마찬가지로 클래스 내 공분산 행렬과 클래스 간 공분산 행렬로 나타낼 수 있다.
$$\textbf{J}(\textbf{W}) = \textbf{Tr}(\textbf{S}_{\textbf{W}}^{-1}\textbf{S}_{\textbf{B}})$$
여기서 클래스 간 공분산 행렬은 전체 공분산 행렬 $S_{\textbf{T}}$를 클래스 내 공분산 행렬을 분해해내고 남은 부분이다.
$$\begin{gather} S_{\textbf{T}} = S_{\textbf{W}}+S_{\textbf{B}} \newline
S_{\textbf{B}} = \sum_{k=1}^{K} N_{k}(\textbf{m}_{k}-\textbf{m})(\textbf{m}_{k}-\textbf{m})^{\textbf{T}} \end{gather}$$
이것은 original $\textbf{x}$ 공간상에서도 투영된 $\textbf{y}$공간 상에서도 나타낼 수 있다. 이 기준을 최대화 하는 값을 구하면 된다. 이 과정이 어렵지는 않다고 하는데 해보지는 못했다.
4.1.7 퍼셉트론 알고리즘(The perceptron algorithm)
고정된 비선형 변환을 통해 특징 벡터 $\phi(\textbf{x})$로 변환 -> 특징 벡터를 사용해 일반화된 선형 모델 $y(\textbf{x})=f(\textbf{w}^{\textbf{T}}\phi(\textbf{x}))$을 만든다. -> 매개변수 $\textbf{w}$를 구한다.
매개변수를 구하는 방식들 중 가장 쉽게 떠올릴 수 있는 것은 오류 함수 최소화이다. 이 때 오분류된 패턴의 총 숫자를 선택하게 되면 오류함수가 piece constant function이 되어서 데이터 중 하나를 건너 이동하는 곳에서 불연속성이 발생하게 된다. 이 경우 기울기가 모든 곳에서 0이 될 것이기 때문에 사용할 수 없다.
퍼셉트론 기준(perceptron criterion)이라는 오류 함수를 사용한다. 예측과 답의 곱에 음수가 많을수록 에러가 커진다. $n$은 오분류된 패턴.
$$ E_{p}(\textbf{w})=-\sum_{n \in M} \textbf{w}^{\textbf{T}}\phi_{n}t_{n}$$
오류 함수에 확률적 경사 하강법을 적용하면 가중 벡터 $\textbf{w}$의 변화는 아래와 같다.
$$\textbf{w}^{(\tau+1)} = \textbf{w}^{(\tau)} - \eta \bigtriangledown E_{p}(\textbf{w}) = \textbf{w}^{(\tau)} - \eta \phi_{n}t_{n}$$
$\eta$는 learning rate, $\tau$는 알고리즘 단계에 대한 지표(몇 번 업데이트)이다. 퍼셉트론 함수는 $f$때문에 $\textbf{w}$에 상수를 곱해도 $y(\textbf{x})$는 변하지 않는다. 따라서 $\eta = 1$로 설정하더라도 일반성을 잃지 않는다.
알고리즘은 아래 그림처럼 단순하게 해석해볼 수 있다. 잘못 분류된 점의 특징벡터를 가중 벡터에 더하는 것.

$K >2$인 클래스에 대해서는 일반화가 되지 않는다.
4.2 확률적 생성 모델(Probabilistic Generative Models)
먼저 사후확률의 표현에 대해 알아보자. 클래스가 두 개인 경우, 클래스 $C_{1}$에 대한 사후 확률을 아래와 같이 적을 수 있다.
$$\begin{align} p(C_{1}|\textbf{x}) &= \frac{p(\textbf{x}|C_{1})p(C_{1})}{p(\textbf{x}|C_{1})p(C_{1})+p(\textbf{x}|C_{2})p(C_{2})} \newline
&= \frac{1}{1+exp(-1)} = \sigma(a)\end{align}$$
$$a= ln \frac{p(\textbf{x}|C_{1})p(C_{1})}{p(\textbf{x}|C_{2})p(C_{2})}$$
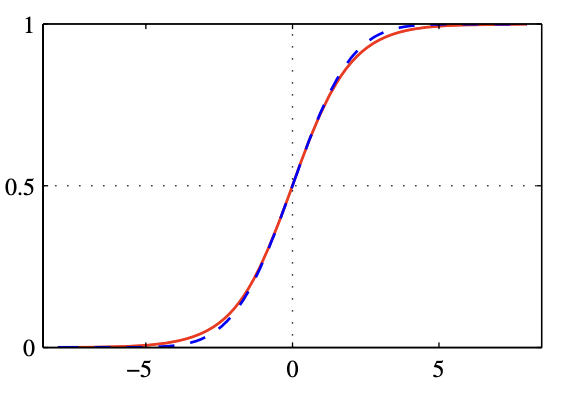
$\sigma(a)$는 로지스틱 시그모이드(logistic sigmoid)함수로서 아래와 같이 정의된다. 전체 실수축을 유한한 범위(이 경우는 [0,1]) 안에 projection하기 때문에 이러한 종류의 함수를 스쿼싱 함수(squashing function)이라고 부르기도 한다.
$$\sigma(a)=\frac{1}{1+exp(-a)}$$
로지스틱 시그모이드 함수의 역은 아래와 같으며 로짓(logit)함수라고 부르기도 한다. $\sigma = p(C_{1}|\textbf{x})$이고 $1-\sigma = 1-p(C_{1}|\textbf{x}) = p(C_{2}|\textbf{x})$이므로 이 함수는 두 클래스에 대한 확률들의 비율이다.
$$a=ln(\frac{\sigma}{1-\sigma})$$
이 때 로그 안의 항을 로그 오즈(log odds)라고 일컫기도 한다.
이것을 확장하여 $K>2$개의 클래스가 있는 경우를 고려하면 아래와 같다.
$$\begin{align} p(C_{k}|\textbf{x}) &= \frac{p(\textbf{x}|C_{k})p(C_{k})}{\sum_{j}p(\textbf{x}|C_{j})p(C_{j})} \newline
&= \frac{exp(a_{k})}{\sum_{j}exp(a_{j})} \end{align}$$
이를 정규화된 지수 함수(nomalized exponential function)이라고 하며, 소프트맥스 함수(softmax function)이라고 하기도 한다. 이때 $a_{k}$는 $a_{k}=\ln (p(\textbf{x}|C_{k}p(C_{k}))$로 정의된다.
4.2.1 연속 입력 - 클래스별 조건부 밀도의 매개변수적 함수 형태 명시
클래스별 조건부 밀도$p(\textbf{x}|C_{k})$가 가우시안이라고 가정하고 그 결과로 사후 확률 $p(C_{k}|\textbf{x})$이 어떤 형태를 가지게 되는지 살펴보자. 모든 클래스들이 같은 공분산 행렬($\Sigma$)을 공유한다고 가정할 것이다(이 가정에 뭔가 근거가 있는지 단순히 계산의 편리함 때문인지 궁금). 따라서 클래스 $C_{k}$에 대한 밀도는 아래와 같다.
$$p(\textbf{x}|C_{k}) = \frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}}exp \{ -\frac{1}{2}(\textbf{x}-\mu_{k})^{\text{T}}\Sigma^{-1} (\textbf{x}-\mu_{k}) \}$$
$a$에 가우시안 분포를 대입해 정리하면 아래와 같은 식을 얻을 수 있다.
$$p(C_{1}|\textbf{x}) = \sigma(\textbf{w}^{\text{T}} \textbf{x}+w_{0})$$
$$\textbf{w} = \Sigma^{-1}(\mu_{1}-\mu_{2})$$
$$w_{0} = -\frac{1}{2} \mu_{1}^{\text{T}} \Sigma^{-1} \mu_{1}+\frac{1}{2} \mu_{2}^{\text{T}}\Sigma^{-1}\mu_{2} +\ln \frac{p(C_{1})}{p(C_{2})}$$
이렇게 구한 결정 경계는 사후 확률이 상수인 경우이며, 결정 경계가 $\textbf{x}$의 선형함수가 될 것이다. 따라서 결정 경계는 입력 공간상에서 선형이다.

$K$개의 클래스의 경우에는 $a$가 아래와 같다. 위의 방식과 유사하게 유도 가능하다.
$$a_{k}(\textbf{x})=\textbf{w}^{\text{T}}\textbf{x}+w_{k0}$$
이 경우 또한 클래스가 두 개일 때와 마찬가지로 결정 경계는 $\textbf{x}$의 선형 함수로 정의된다.
4.2.2 최대 가능도 해 - 매개변수들의 값과 사전 클래스 확률
4.2.1에서 처럼 클래스 조건부 밀도 $p(\textbf{x}|C_{k})$를 명시하고 나면 최대 가능도 방법으로 매개변수와 사전 클래스 확률 $p(C_{k})$를 구할 수 있다. 이를 위해서 관측값 $\textbf{x}$와 클래스 라벨로 이루어진 데이터 집합 $\{ \textbf{x}_{n}, t_{n} \}$ 필요하다.
두 개의 클래스가 있는 경우를 생각해보자. $p(\textbf{x}|C_{k})$가 가우시안 밀도를 가지고, 공부산 행렬은 공유한다고 가정하자. 클래스 $C_{1}$인 경우 $t_{n}=1$, 클래스 $C_{2}$인 경우 $t_{n}=0$이다. 사전 클래스 확률 $p(C_{1})=\pi$라고 하자.
가능도 함수는 아래와 같이 주어진다. 모든 데이터에 대해 정답 라벨이 출력될 확률을 곱한 것이다. 만약 분류가 잘못 되었다면 해당 라벨이 출력될 확률이 작을 것이므로 가능도 함수가 작아진다(라고 보는게 맞나..?).
$$p(\textbf{t},\textbf{X}|\pi, \mu_{1}, \mu_{2}, \Sigma) = \prod_{n=1}^{N}[\pi \mathcal{N}(\textbf{x}_{n}|\mu_{1}, \Sigma)]^{t_{n}}[(1-\pi) \mathcal{N}(\textbf{x}_{n}|\mu_{2}, \Sigma)]^{1-t_{n}}$$
이 가능도 함수가 최대가 되는 $\pi, \mu_{1}, \mu_{2}, \Sigma$ 각각을 구해 가능도 함수를 최대화 한다. 가능도 함수의 로그를 취한 후, 미분값을 0으로 놓는 방식으로 최대화 하는 값을 구하게 된다.
$$ln(p(\textbf{t},\textbf{X}|\pi, \mu_{1}, \mu_{2}, \Sigma)) = \sum_{n=1}^{N}\{ t_{n}\ln \mathcal{N}(\textbf{x}_{n}|\mu_{1}, \Sigma) + (1-t_{n})\ln \mathcal{N}(\textbf{x}_{n}|\mu_{2}, \Sigma) \}$$
$\pi$에 대한 최대화
위의 식에서 $\pi$에 종속적인 부분만 남기면 $\sum_{n=1}^{N}\{ t_{n}\ln\pi +(1-t_{n})\ln(1-\pi) \}$이 된다. $\pi$에 대한 미분값을 0으로 놓고 정리하면 아래와 같다.
$$\pi = \frac{1}{N}\sum_{n=1}^{N} t_{n}=\frac{N_{1}}{N}=\frac{N_{1}}{N_{1}+N_{2}}$$
$\pi$에 대한 최대화는 클래스면 데이터 크기와 관련되어있어 클래스가 여러개 있는 경우에도 쉽게 일반화가 가능하다.
$\mu$에 대한 최대화
마찬가지로 $\mu_{1}$에 대해서 최대화해 보자. 로그 가능도 함수에서 $\mu_{1}$에 종속적인 항만 남기면 아래와 같다.
$$\sum_{n=1}^{N} t_{n}\ln \mathcal{N}(\textbf{x}_{n}|\mu_{1}, \Sigma) = -\frac{1}{2}\sum_{n=1}^{N}t_{n}(\textbf{x}_{n}-\mu_{1})^{\mathbf{T}}\Sigma^{-1}(\textbf{x}_{n}-\mu_{1}) + \text{const}$$
$\mu_{1}$에 대한 미분값을 0으로 놓고 정리하면 다음을 구할 수 있다.
$$\mu_{1}=\frac{1}{N_{1}}\sum_{n=1}^{N}t_{n}\textbf{x}_{n}$$
비슷한 방법으로 $\mu_{2}$에 대한 결과를 구하면 아래와 같다.
$$\mu_{2}=\frac{1}{N_{2}}\sum_{n=1}^{N}(1-t_{n})\textbf{x}_{n}$$
$\Sigma$에 대한 최대화
$\Sigma$에 종속적인 항만 선택하면 아래와 같다.
$$\begin{align} &-\frac{1}{2}\sum_{n=1}^{N}t_{n}\ln |\Sigma|-\frac{1}{2}\sum_{n=1}^{N}t_{n}(\textbf{x}_{n}-\mu_{1})^{\mathbf{T}}\Sigma^{-1}(\textbf{x}_{n}-\mu_{1})-\frac{1}{2}\sum_{n=1}^{N}(1-t_{n})\ln |\Sigma|-\frac{1}{2}\sum_{n=1}^{N}(1-t_{n})(\textbf{x}_{n}-\mu_{2})^{\mathbf{T}}\Sigma^{-1}(\textbf{x}_{n}-\mu_{2}) \newline
&=-\frac{N}{2}\ln | \Sigma | -\frac{N}{2}Tr\{ \Sigma_{-1}\textbf{S} \} \end{align}$$
$\textbf{S}=\frac{N_{1}}{N}\textbf{S}_{1}+\frac{N_{2}}{N}\textbf{S}_{2}$이고, $\textbf{S}_{n}$은 각 클래스의 분산이다. 위의 식을 $\Sigma$에 대해 미분하여 그 값이 0인 경우를 찾으면 $\Sigma = \textbf{S}$이다.
공분산 공유하는 $K$ 클래스로 확장 가능하다. 책의 연습문제 4.10을 참고하면 된다.
4.2.3 이산 특징
두 개의 클래스를 가지는 경우 이산일 때 클래스 조건부 분포는 아래와 같다.
$$p(\textbf{x}|C_{k})=\prod_{i=1}^{D}\{ \mu_{ki}^{x_{i}}+(1-\mu_{ki})^{1-x_{i}} \}$$
이 식을 위에 $a_{k}$관한 식에 대입하면 아래와 같다.
$$a_{k}(\textbf{x})=\sum_{i=1}^{D}\{ x_{i}\ln\mu_{ki}+(1-x_{i})\ln(1-\mu_{ki}) \} +\ln(C_{k})$$
4.2.4 지수족
지금까지는 가우시안 분포를 가정했다. 보다 일반적인 경우인 지수족 분포라고 가정했을 때 결과를 알아보자.
지수족 분포의 정의에 따라 $\textbf{x}$에 대한 분포를 다음의 형태로 적을 수 있다.
$$p(\textbf{x}| \lambda_{k})=h(\textbf{x})g(\lambda_{k})exp\{ \lambda_{k}^{\text{T}}\textbf{u}(\textbf{x}) \}$$
이러한 분포 중 $\textbf{u}(\textbf{x}) = \textbf{x}$인 부분 집합들에서만 고려하고, 척도 매개변수(scale parameter) $s$를 도입해 아래와 같은 제한된 형태의 지수족 분포 클래스 조건부 밀도를 구할 수 있다. 척도 매개변수는 공유한다고 가정하자.
$$p(\textbf{x}| \lambda_{k}, s)=\frac{1}{s} h(\frac{1}{s}\textbf{x})g(\lambda_{k})exp\{ \frac{1}{s}\lambda_{k}^{\text{T}}\textbf{u}(\textbf{x}) \}$$
클래스가 $K$개인 경우, 아래와 같은 식을 구할 수 있다. 이것은 $\textbf{x}$에 대해 선형함수이다.
$$a_{k}(\textbf{x})=\frac{1}{s}\lambda_{k}^{\text{T}}\textbf{x}+\ln g(\lambda_{k}) + \ln p(C_{k})$$
'Deep Learning' 카테고리의 다른 글
- depth
- TRACKING
- Generative Model
- pcb
- feature
- 신호처리
- OS
- Depth estimation
- 딥러닝
- machine learning
- 운영체제
- ML Pipeline
- Gan
- mode collapse
- conditional GAN
- 3d object detection
- depthmap
- Building Basic GAN
- ML
- AI
- Deep learning
- design pattern
- Operating System
- MLOps
- DSP
- 디지털신호처리
- Raspberry Pi
- controllable GAN
- image
- deeplearning
- Total
- Today
- Yesterday
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
