 Unsupervised learning of depth and ego-motion from video
Unsupervised learning of depth and ego-motion from video
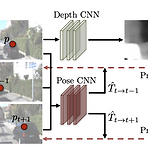
이 논문은 unsupervised한 방법으로 image depth를 구하는 모델을 학습시키는 방법이다. 학습에는 sequential한 이미지가 필요하고, 각 이미지의 pose를 이용해 한 이미지의 point들을 다른 이미지로 projection하고, projection된 위치의 점과 Intensity를 비교해 loss를 구한다. 여기서 pose도 model output이므로 gt없이 loss 계산이 가능해진다. Overview 조금 더 구체적으로 살펴보면 다음과 같은 단계로 나누어 생각해 볼 수 있다. 1. t에서의 이미지 It를 depth CNN에 통과시켜 Depthmap ^Dt(p)를 구한다.(Depth map은 모든 이미지 픽셀에 대한 depth를 가지고 있다.) 2...
 Digital Filter Structure
Digital Filter Structure
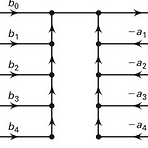
Filter라고 하는 어떤 system을 디자인하고 구현 할 때, filter structure를 통해 실제로 어떻게 구현할 것이며, 어떻게 디자인할 것인지를 고려해볼 수 있습니다. Basic Elements 이 포스팅에서는 LTI system을 고려하며, filter structure는 아래와 같은 요소들로 구성됩니다. Adder: 두 선이 만나는 점으로 표현된다. Multiplier(gain): 화살표 위에 적힌 값을 곱해준다. Delay element (shift or memory): 화살표 위에 z−k가 적혀있다면, k만큼 shift된 것이다. IIR Filter Structure IIR(Infinite-duration Impulse Response) filter는 입력신호의 값과 출..
 Z-transform
Z-transform
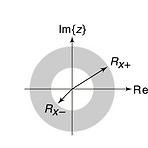
Fourier Transform에는 두 가지 단점이 있다. DTFT가 존재하지 않는 여러 유용한 signal들이 존재한다. 예를 들어, u(n), nu(n)과 같은 신호들은 absolutely summable하지 않아서 DTFT가 존재하지 않는다. 또한, 초기 조건이나 input의 변화로 인한 system의 transient response(변화 대응해 steady-state로 가기전 과도기적 상태)를 DTFT에서는 반영하지 못한다. 이러한 두 가지 문제를 해결하기 위해 DTFT의 확장 형태인 z-transform이 나오게 되었다. Bilateral z-transform Definition $$ X(z)\equiv \sum_{n=-\infty}^{\infty} x(n)z^{-n}, R_{-} < ..
 DTFT(Discrete-Time Fourier Transform)
DTFT(Discrete-Time Fourier Transform)
Discrete-Time Fourier Transform은 Discrete Time domain 신호를 Continuous frequency domain으로 옮기는 방법이다.(나중에 DFT가 나오는데 서로 다른 것이니 헷갈리지 말것!) 신호라는 것을 배워본 적이 없어서 time domain과 frequency domain을 이해하는것도 어려웠는데 유튜브 영상이 도움이 되었다. fourier transform을 시각적으로 보여주는 영상인데 time domain에서의 신호가 복소평면(z-plane)에서 어떻게 그려지는지 보여주고 그것을 frequency domain의 그래프로 다시 그리는 것을 보여준다. (몰랐는데 한국어 번역 영상도 존재한다.) Definition of DTFT x(n) 은 time d..
- Generative Model
- ML
- Depth estimation
- controllable GAN
- AI
- MLOps
- image
- depth
- 딥러닝
- Raspberry Pi
- design pattern
- Operating System
- ML Pipeline
- 디지털신호처리
- 운영체제
- 3d object detection
- DSP
- machine learning
- depthmap
- conditional GAN
- OS
- Gan
- Deep learning
- mode collapse
- TRACKING
- deeplearning
- Building Basic GAN
- feature
- 신호처리
- pcb
- Total
- Today
- Yesterday
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
